단순한 지도 만들기

인포그래픽에서는  사용하는 지도는 실제에 가까운 것보다는 단순한 형태 위에 문자나 숫자를 표시해야 가독성이 좋습니다.    복잡한 곡선을  단순한 몇 개의 직선으로 바꾸어 주는 프로그램으로   Ramer-Douglas-Peucker 알고리즘(이하 RDP)이 있습니다.   한 개의 선으로 된 곡선은 문제가 없지만 지도와 같이 연결점이 많은 그림에서는 아래와 같이 엉망이 됩니다.

             

연결점을 찾고 연결점과 연결점 사이에만 RDP를 적용하면 단순한 지도를 만들 수 있습니다.  아래 그림은 서울 마포구입니다.  적색점이 다른 구와의 연결점으로 7개가 있습니다.  7개 연결하는 각 곡선에 대해 RDP를 적용해서 곡선이 아닌 직선 몇 개로 구성된 선을 그립니다.  

https://github.com/yoojchul/rdp-for-polygon 에 있는 전체 프로그램 순서도 그러합니다.   연결점을 찾고 연결점 사이의 경계선을 단순화합니다.  프로그램 아래 부분은 json 파일이 들어 있는 위도와 경도를 소수 4번째만 남겨 놓습니다.    

polygons = []
pts=[]    # decrease resolution to four decimal places
for  feature in geoJSON['features']:
    pts = []
    prev_x = 0
    prev_y = 0
    for p in feature['geometry']['coordinates'][0]:
        x = round(p[0], 4)
        y = round(p[1], 4)
        if x == prev_x and y == prev_y:
            continue
        pts.append([x, y, 0])
        prev_x = x
        prev_y = y
    polygons.append(pts)

각 점은 리스트로 기록하는데 첫번째 요소는 x축(경도),  두번째 요소는 y축(위도),  세번째 요소는  인접도입니다.   아래 부분은 인접도를 계산하는 프로그램입니다.

# accumulate neighbor in three decimal plances 
cum = {} 
for pl in polygons:
    visited = {}
    for p in pl:
        dot = (round(p[0], 3), round(p[1], 3))
        if dot in visited:
            visited[dot] += 1
        else:
            visited[dot] = 1
        if dot in cum:
            if visited[dot] == 1:   #  to prevent p in same pl
                cum[dot] += 1
        else:
            cum[dot] = 1
# assign neighbor counter to 3rd 
for pl in polygons:
    for p in pl:
        p[2] = cum[(round(p[0], 3), round(p[1], 3))]

반올림해서 소수 3번째 자리까지가 같으면 같은 경계선 위에 있는 것으로 간주합니다.    이렇게 계산하는 이유는 같은 경계선에 있다고 하더라도 위도와 경도가 행정구역마다 다르기 때문입니다.  아래 그림에서  곡선은 행정구역의 경계선이지만 청색은 A 행정구역을 표시할 때 사용한 경계점이고 적색은 B 행정구역을 표시한 경계점으로  일치하는 않은 경우가 태반입니다.   이들 경계점들은 두 행정구역 사이에 있으므로 인접도는 2이어야 합니다.

인접도를 이용해서 선의 연결점을 찾는 프로그램입니다.  

# find _joints_ where lines meet
joints = []
for  pl in polygons:
    multi = pl[0][2]
    prev =[p[0], p[1]]
    for p in pl[1:]:
        if multi < p[2]: # branch
            if not [p[0], p[1]] in joints:
                joints.append([p[0], p[1]])
        elif multi > p[2]:  # combine
            if not prev in joints:
                joints.append(prev)
        prev = [p[0], p[1]]
        multi = p[2]
x = []
y = []
for p in joints:
    x.append(round(p[0], 3))
    y.append(round(p[1], 3))
#ax.plot(x, y, 'o', color='red')

인접도의 차이가 발생하는 곳은 선의 연결점입니다. 아래 그림은 세 행정구역이 만나는 영역인데  선위의 숫자는 인접도를 의미합니다.  2에서 3으로 바뀐 곳이 연결점입니다.

이렇게 찾은 인접도와 연결점을 이용해서 연결점 사이의 점들(연결점 포함) pts에 옮기고 rdp()를 호출하여 곡선을 간략하게 만듭니다.

for  pl in polygons:
    multi = pl[0][2]
    pts = []
    if [pl[0][0], pl[0][1]] in joints: # to merge to joints
        pts.append([round(pl[0][0], 3), round(pl[0][1], 3)])
        prev = [round(pl[0][0], 3), round(pl[0][1], 3)]
    else:
        pts.append([pl[0][0], pl[0][1]])
        prev = [pl[0][0], pl[0][1]]
    for p in pl[1:]:  # from 2nd 
        if multi != p[2]:
            if multi < p[2]:  # 1-1-2
                min_dist =  100.0
                min_idx = 0
                for idx, val in enumerate(joints):   # find nearest joints
                    dist =  abs(val[0] - prev[0]) + abs(val[1] - prev[1])
                    if min_dist > dist:
                        min_idx = idx
                        min_dist = dist
                pts.append([round(joints[min_idx][0], 3),  round(joints[min_idx][1], 3)])
            rdp_pts = rdp(pts, epsilon=0.01)
            x = [i for i, j in rdp_pts]
            y = [j for i, j in rdp_pts]
            ax.plot(x, y, color='gray')
            pts = []
            if multi > p[2]:  # 2-2-1
                pts.append(prev)
        if [p[0], p[1]] in joints: # to merge to joinsts
            pts.append([round(p[0], 3), round(p[1], 3)])
            prev = [round(p[0], 3), round(p[1], 3)]
        else:
            pts.append([p[0], p[1]])
            prev = [p[0], p[1]]
        multi = p[2]

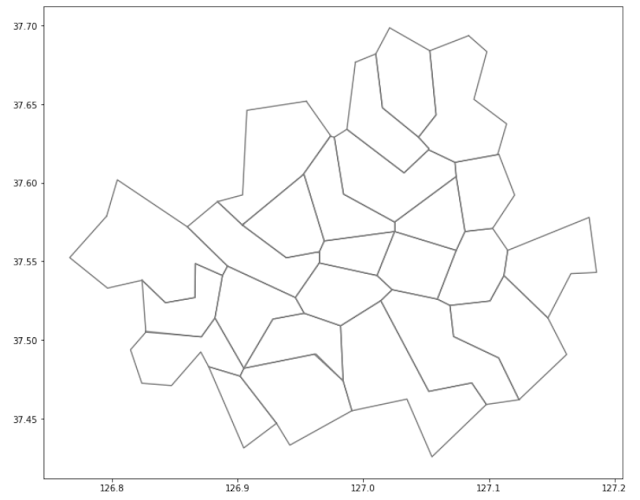
아래 그림이 최종 결과입니다.